Seeing sharper with electrons
The aim to achieve ideal focusing of glass lenses or the problem to compensate for their aberrations, respectively, dates back about 800 years. Towards the end of the 19th century, Abbe developed the theory of image formation in the microscope and provided a scientific basis for the fabrication of microscopes. In 1873, he published his fundamental work on the resolution limit of optical microscopes after he had realized that diffraction determined the achievable resolution [ABB73]. Assuming a perfect lens, he showed that the resolution limit is given by
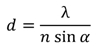
Here λ is wavelength, α is the aperture angle and n is the refraction index. This formula is quite universal because it also holds for electron microscopes where the usable aperture angle depends on the aberrations1. One major achievement in the design of optimum compound lenses was the replacement of the extensive trial and error process by precise calculations of the objective lenses. The new wave theory of optics provided a formal and sufficient basis for the engineering of lenses. As a result, apochromats [ABB86] have been designed which are corrected for three colors. The performance of these lenses was significantly better than that of any previous objective lens. The optical community owes Ernst Abbe not less than 50 important inventions and discoveries. Due to the development of advanced fabrication techniques by Abbe and Zeiss at the beginning of the 20th century, microscope fabrication was concentrated in Germany at that time.
In 1926, the focusing property of rotationally symmetric magnetic fields was discovered and analyzed by H. Busch. He showed theoretically that a coil carrying a current deflects electrons in the same way as a glass lens refracts the light rays. The lens equation of the light optics can thus also be applied to electrons making it the basis of electron optics. The equation for a short lens is
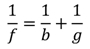
Here f, b and g are the focal length, the distance between lens and image and the distance between lens and object, respectively. Unlike a glass lens, whose refracting surfaces can be shaped as desired, the electromagnetic field of an electron lens is determined by Maxwell’s equations and cannot be formed arbitrarily. This constraint results in lens aberrations which prevent perfect imaging and thus limit the performance of the microscope. The spherical aberration arises in light optics when lenses or mirrors with spherical surfaces are used. This aberration broadens the image of each object point. Based on the pioneering work of H. Busch, it became possible to calculate the paths of electrons in magnetic fields, in particular the focusing properties of coils encapsulated in iron.
These short magnetic lenses are the basic elements of all electron microscopes. After studying the Busch formula for the focal length of magnetic lenses, Knoll and Ruska developed the first single-stage magnetic electron microscope. A short time later, they built a two-stage instrument and named it transmission electron microscope (TEM)2. Already in 1934, the resolution of the TEM surpassed that of the light microscope [BOR38].
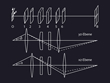
The development of the electron microscope was accompanied by theoretical studies of the properties of electron lenses, multipoles and other electron optical components. In 1936, Scherzer found the so-called "Scherzer theorem" [SCH36] which states that the spherical and the chromatic aberrations of static rotationally symmetric and space-charge-free electron lenses are unavoidable if the object and image are real. Spherical aberration of round lenses is always positive because the marginal rays, which intersect the outer zones of the lens, are always more deflected than the paraxial rays, as shown in Fig. 1 [NEL05]. Scherzer himself showed theoretically, in 1947, that the aberrations can be corrected by lifting any one of the constraints of his theorem. Scherzer has made many ingenious fundamental contributions to the correction of spherical and chromatic aberration of electron lenses. Therefore, he is quite often called "the father of aberration correction" [MSA11]. Nevertheless, he had to defend the validity of his theorem against critics from his competitor W. Glaser who asserted that the theorem was erroneous by proposing a magnetic electron lens free of spherical aberration [GLA40]. In 1941, Recknagel showed that the magnetic field of this lens does not provide a real image and thus does not fulfill the conditions required for the validity of the Scherzer theorem [REC41].
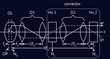
Scherzer proposed several correction procedures (Fig. 2), in particular the CS-corrected system shown in Fig. 3 [SCH47]. At Scherzer’s time computers were not yet available and numerical calculations very time consuming.
From 1948 onwards, theoretical studies and experiments on aberration correction were conducted at Scherzer’s institute in Darmstadt over a period of many years [ROS08]. In 1951, Seeliger showed experimentally that the Scherzer corrector (Fig. 3) compensated for the spherical aberration of the objective lens. However, he could not improve the resolution limit of the basic electron microscope due to electrical and mechanical instabilities of the corrector elements [SEE51].
In 1953, Scherzer’s corrector design was used as a basis for correction efforts in England. Archard proposed to substitute four quadrupoles for the two cylinder lenses and the inner round lens of the Scherzer corrector in order to achieve a higher mechanical stability [ARC54]. However, also this corrector could not improve the resolution of the electron microscope.
In 1956, Moellenstadt made further experiments with the Scherzer-Seeliger corrector in Tübingen [MOE56]. By employing critical illumination with a large cone angle of 20 mrad, he increased the spherical aberration to such an extent that it became by far the most dominant aberration blurring severely the image. After compensating for the spherical aberration by the octopoles, the resolution improved by a factor of about 7 accompanied by a remarkable improvement in contrast.
In 1957, Scherzer advised his PhD student Meyer to examine the obstacles that limit the actual resolution of the spherical-aberration-corrected electron microscope. In his thesis Meyer investigated both theoretically and experimentally the requirements for achieving an improvement in resolution by correction of aberrations [MEY61]. He realized that two kinds of parasitic aberrations prevented an improvement of resolution: (1) adjustment aberrations resulting from poor alignment, lens imperfections and insufficient shielding of static external fields and (2) time-dependent aberrations caused by electrical and mechanical instabilities and by insufficient shielding of external alternating fields [MEY61].
In another thesis performed at Scherzer‘s institute, Tretner determined the lower limit of the coefficients CS and CC of spherical and chromatic aberration for several constraints [TRE59]. His results have subsequently been utilized by Riecke for designing the so-called condenser-objective lens which minimizes CS and CC [RIE66]. This lens is still used in most high-resolution electron microscopes and enables a resolution of about 100λ for non-corrected microscopes [ROS08].
Although Scherzer could show that the departure from rotational symmetry is sufficient to eliminate chromatic aberration, no practical corrector could be found up to 1961 when Kelman showed that the combined electrostatic-magnetic quadrupole can have a chromatic aberration coefficient with negative sign opposite to that of a round lens [KEL61]. In 1967, Hardy first obtained experimentally a negative chromatic aberration with a system of four electric-magnetic quadrupoles [HAR67]. However, it remained a proof of principle because the system could not be used as a corrector for an electron microscope. The successful correction of chromatic aberration in an actual electron microscope was first demonstrated within the frame of the so-called Darmstadt Project by means of a novel corrector. It enabled compensation of chromatic and spherical aberration [KOO77] in 1976. This corrector was composed of three magnetic quadrupoles, two electric-magnetic quadrupoles and three octopoles.
During their experiments Scherzer, Rose and co-workers had systematically eliminated the parasitic aberrations which had prevented the successful aberration correction.
In 1963, Dymnikov showed that a symmetric quadrupole quadruplet with anti-symmetric excitation of the quadrupoles can be used as a substitute for a round lens [DYM63]. Later improved versions of this system served as correctors [ROS71, BEC74, ZAC95, KRI98]. The so-called Chicago-corrector consisting of four magnetic quadrupoles and octopoles was built and tested in the scanning transmission electron microscope (STEM) from 1972 to 1978 [BEC74]. Also this corrector failed to improve the resolution of the STEM.
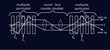
In 1965, Hawkes discovered that sextupoles produce rotationally symmetric third-order combination aberrations apart from other aberrations [HAW65]. His findings remained largely unnoticed until 1979 when Beck showed that a combination of a single round lens and two sextupoles is able to produce a negative spherical aberration [BEC79]. Unfortunately, his systems introduced a large fourth-order aperture aberration which prevents an appreciable improvement in resolution [BEC79, CRE80]. Subsequent studies showed that hexapoles are suitable elements for nullifying successfully CS because the correctors require fewer elements and can be adjusted more easily than quadruple-octopole correctors [ROS81, CRE82, SHA88, CHE91]. In 1990, H. Rose proposed the semi-aplanat depicted in Fig. 4 which is composed of the objective lens, two round-lens transfer doublets and two hexapoles [ROS90].
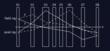
In 1997, Haider and co-workers finally achieved the breakthrough in practical aberration correction by improving the point resolution of their 200kV TEM from 2.4 A to 1.4 A [HAI97]. The realization of the Rose corrector and the successful correction of the spherical aberration by his former students was achieved within a period of less than 10 years at the EMBL in Heidelberg [HAI98a,b,c]. Subsequently, the corrected CM200FEG TEM was transferred to the Research Center Jülich where it provides genuine atomic resolution images up to this day [JIA03, JIA04, HOU09]. By improving the mechanical and the electric stability of the elements and by reducing the contamination, the resolution limit of corrected TEMs has been further lowered to 0.1 nm [HAI08]. After the correction of the spherical aberration, the correction of the chromatic aberration remained an open issue. In order to avoid blurring of the image, electrons with different energies must intersect the same image point, as illustrated in Fig. 1b. To enable simultaneous correction of spherical and chromatic aberration (see Fig. 1c), it is necessary to replace each sextupole by a quintupled composed of quadrupole and octopole elements (Figs. 5, 6). The successful correction of spherical and chromatic aberration [ROS05] improved the resolution to 0.05 nm at 300 kV [KIS08]. Today, transmission electron microscopy with full (chromatic and spherical) aberration correction aims to the investigation of sensitive materials, for which we go to primary energies from 20 to 80 kV [KAI11]. Harald Rose and Ute Kaiser from Ulm University together with the companies CEOS and FEI have realized the fully aberration corrected low voltage sub-Å transmission electron microscope SALVE III with a resolution record of 15 x wavelength (90 pm at 40 kV) [LIN16]. This so-called Rose-Kuhn corrector is schematically shown in Fig. 7.
Footnotes:H. Boersch (1909 - 1986) showed that Abbe’s theory of image formation in the light microscope also holds for the electron microscope.
M. Knoll and E. Ruska built the first two-stage microscope in 1931 after they realized the focusing properties of solenoids.
[ABB73] Abbe, E. (1873) Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Archiv für mikroskopische Anatomie, 9: 413-418
[ABB86] Abbe, E. (1887) On Improvements of the Microscope with the aid of New Kinds of Optical Glass. J. Roy. Microsc. Soc. , 7: 20-34, original paper in German: (1886) Cf. SB. Jen. Gesell. f. Med. u. Naturw, 9. Jul.: 24pp
[ARC54] Archard, G. D. (1954) Requirements contributing to the design of devices used in correcting electron lenses. Br. K. Appl. Phys., 5: 294-299
[BEC74] Beck, V. D. and A. Crewe (1974) A quadrupole octopole corrector for a 100 kV STEM. Proc. Ann. Meeting EMSA, 32: 426-427
[BEC79] Beck, V. D. (1979) A hexapole spherical aberration corrector. Optik, 53: 241-255
[BOR38] von Borries, B. und E. Ruska: Das Übermikroskop als Fortsetzung des Lichtmikroskops. (1938) In: Proc. German naturalists and physicians, 95: 72-77, Meeting in Stuttgart on 18 - 21 September
[CHE91] Chen, E. , and C. Mu (1991) New development in correction of spherical aberration of electro-magnetic round lens. In: Proc. Int. Symp. Electron Microscopy, K. Kuo and J. Yao (eds.): 28-35. Singapore: World Scientific.
[CRE80] Crewe, A. V. (1980) Studies on sextupole correctors. Optik, 57: 313-327
[CRE82] Crewe, A. V. (1982) A system for the correction of axial aperture aberrations in electron lenses. Optik, 60: 271-281
[DYM63] Dymnikov, A.D., and Yavor, S.Ya. (1963) Four quadrupole lenses as an anlogue of an axially symmetric system. Sov. Phys. Tech. Phys., 8: 639-643
[ERN10] Erni, R., (2010) Aberration-corrected Imaging in Transmission Electron Microscopy: An Introduction. Imperial College Press, London
[FRA17] von Fraunhofer, J. (1817) Bestimmung des Brechungs- und des Farbenzerstreungs-Vermögens verschiedener Glasarten, in Bezug auf die Vervollkommnung achromatischer Fernröhre. Annalen der Physik, 56: 264-313
[GLA40] Glaser, W. (1940) Ueber ein von sphaerischer Aberration freies Magnetfeld. Z. Phys., 116: 19-33; 734-745
[HAI97] Haider, M. and S. Uhlemann (1997) Seeing is not believing: Reduction of artefacts by an improved point resolution with a spherical aberration corrected 200 kV transmission electron microscope. Microsc. Microanal., 3 (Supplement 2): 1179-1180
[HAI98a] Haider, M., Rose, H., Uhlemann, S., Schwan, E., Kabius, B., and Urban, K. (1998) Towards 0.1 nm resolution with the first spherically corrected transmission electron microscope. J. Electron Microsc., 47: 395-405
[HAI98b] Haider, M., H. Rose, S. Uhlemann, E. Schwan, B. Kabius, and K. Urban (1998) A spherical-aberration-corrected 200 kV transmission electron microscope. Ultramicroscopy, 75: 53-60
[HAI98c] Haider, M., S. Uhlemann, E. Schwan, H. Rose, B. Kabius, and K. Urban (1998) Electron microscopy image enhanced. Nature, 392: 768-769
[HAI08] Haider, M., H. Müller, S. Uhlemann, J. Zach, U. Loebau, and R. Hoeschen (2008) Prerequisites for a CC/CS-corrected ultrahigh resolution TEM. Ultramicroscopy, 108: 167-178
[HAR67] Hardy, D. F. (1967) Combined magnetic and electrostatic quadrupole electron lenses. Dissertation, Cambridge
-
[HAW65] Hawkes, P. W. (1965), The geometrical aberrations of general electron optical systems. I and II (two paper) Philosophical Transactions of the Royal Society A, 257: 479-552
[HOU09] Houdellier, F. (2009) La correction d’aberration sphérique image: applications en imagerie et diffraction. Societé française des microscopies SFMU 2009, Assemblée générale June 2009Paris, France
[JIA03] Jia, C.L., M. Lentzen, and K. W. Urban (2003) Atomic-resolution imaging of oxygen in perovskite ceramics. Science, 299: 870-873
[JIA04] Jia, C. L., M. Lentzen, and K. Urban (2004) High-resolution transmission electron microscopy using negative spherical aberration. Microsc. Microanal., 10: 174-184
[KAI11] Kaiser, U. A. , J. Biskupek, J. C. Meyer, J. Leschner, L. Lechner, H. Rose, M. Stöger-Pollach, N. Khlobystov, P. Hartel, H. Müller, M. Haider, S. Eyhusen, and G. Benner (2011) Transmission electron microscopy at 20 kV for imaging and spectroscopy. Ultramicroscopy, 111: 1239-1246
[KEL61] Kelman, V. M., and Yavor, S. Ya (1961) Achromatic quadrupole electron lenses. Zh. Tekh. Fiz., 31: 1439-1442
[KIS08] Kisielowski, C., B. Freitag, M. Bischoff, H. van Lin, S. Lazar, G. Knippels, P. Tiemeijer, M. van der Stam, S. von Harrach, M. Ste- kelenburg, M. Haider, H. Muller, P. Hartel, B. Kabius, D. Miller, I. Petrov, E. Olson, T. Donchev, E. A. Ke- nik, A. Lupini, J. Bentley, S. Pennycook, A. M. Minor, A. K. Schmid, T. Duden, V. Radmilovic, Q. Ramas- se, R. Erni, M. Watanabe, E. Stach, P. Denes, and U. Dahmen (2008) Detection of single atoms and buried defects in three dimensions by aberration-corrected electron microscopy with 0.5 Å information limit. Microsc. Microanal., 14: 454-462
[KOO77] Koops, H., G. Kuck and O. Scherzer (1977) Erprobung eines elektronenoptischen Achromators. Optik, 48: 225-236
[KRI98] Krivanek, O. L. , N. Dellby and L. M. Brown (1998) Spherical aberration corrector for a dedicated STEM. Proceedings of EUREM-11, the 11th European Conference on Electron Microscopy, Dublin 1996 (CESEM, ed.), Brussels, 1: 352-353
[LIN16] Linck, M., Hartel, P., Uhlemann, S., Kahl, F., Müller, H., Zach, J., Haider, M., Niestadt, M., Bischoff, M., Biskupek, J., Lee, Z., Lehnert, T., Börrnert, F., Rose, H. H. & Kaiser, U. A. (2016). Chromatic Aberration Correction for Atomic Resolution TEM Imaging from 20 to 80 kV. Physical Review Letters, 117: 076101
[LIS43] Lister, J. L., (1843) On the Limit to Defining Power in Vision with the Unassisted Eye, the Telescope and the Microscope. unpublished
[MEY61] Meyer, W. E. (1961) Das praktische Aufloesungsvermoegen von Elektronenmikroskopen. Optik, 18: 101-114
[MOE56] Moellenstedt, G. (1956) Elektronenmikroskopische Bilder mit einem nach O. Scherzer sphaerisch korrigierten Objektiv. Optik, 13: 209-215
[MSA11] MSA Microscopy Society of America. (2011) Scherzer, O. 1909-1982, Biography and historical Poster
[NEL05] Nellist, P. D. (2005) Seeing with electrons. Physics World, 18: 24-29
[REC41] Recknagel, A. (1941) Ueber die sphaerische Aberration bei elektronenoptischer Abbildung. Z. Physik, 117: 67-73
[RIE66] Riecke, W. D. and E. Ruska (1966) A 100-kV transmission electron microscope with single-field condenser objective. Proceedings of the 6th International Congress on Electron Microscopy, 1: 19-20
[ROS71] Rose, H. (1971) Abbildungseigenschaften sphärisch korrigierter elektronenoptischer Achromate. Optik, 33: 1-24
[ROS81] Rose, H. (1981) Correction of aperture aberrations in magnetic systems with threefold symmetry. Nucl. Instrum. Meth., 187: 187-199
[ROS90] Rose, H. (1990) Outline of a spherically corrected semi-aplanatic medium-voltage TEM. Optik, 85: 19-24
[ROS05] Rose H. (2005) Prospects for aberration-free electron microscopy. Ultramicroscopy, 103: 1-6
[ROS08] Rose, H. (2008) Optics of high-performance electron microscopes. Science and Technology of Advanced Materials, 9: 014107
[ROS09c] Rose, H. (2009) Geometrical Charge-Particle Optics. Springer Series in Optical Sciences, 142, Springer Berlin Heidelberg
[RUS37] Ruska, E. (1937) Elektronenmikroskop und Übermikroskop. In: Contributions to Electron Microscopy, presentations from the Conference on Physics 1936, (Eds.) H. Busch und E. Brüche, (Publ.) , Johann Ambrosius Barth, Leipzig
[SCH36] Scherzer, O. (1936) Über einige Fehler von Elektronenlinsen. Z. Physik, 101: 593-603
[SCH47] Scherzer, O. (1947) Spherical and chromatic correction of electron lenses. Optik, 2: 114-132
[SEE51] Seeliger, R. (1951) Die sphaerische Korrektur von Elektronenlinsen mittels nicht rotationssymmetrischer Abbildungselemente. Optik, 8: 311-317
[SHA88] Shao, Z. (1988) Correction of spherical aberration in transmission electron microscope. Optik, 80: 61-75
[TRE59] Tretner, W. (1959) Existenzbereiche rotationssymmetrischer Elektronenlinsen. Optik, 16: 155-184
[ZAC95] Zach J., and M. Haider (1995) Correction of spherical and chromatic aberration in a low-voltage SEM. Optik, 99: 112-118