Atom migration in MoTe₂

Figure 1. MoTe₂ at 40 kV.

Figure 2. Te vacancy line at 40 kV.

Figure 3. Migration of vacancies

Figure 4. Phase transformation.

Figure 5. 1H-MoTe₂

Figure 6. Vacancy formation energies

Figure 7. 1T'-phase islands

Figure 8. Phase transformations

June 14, 2021 - Tailoring the local optical and electronic properties of 2D TMDs is a long standing challenge in materials science. Two research groups at the University of Ulm, the Helmholtz-Center Dresden-Rossendorf in Germany and the University of Aalto in Finland have published new findings on atom migrations in single-layer 1H-MoTe₂ in the transmission electron microscope at an electron energy of 40 keV, which should facilitate tailoring the local properties of the material.

Low-voltage aberration-corrected transmission electron microscopy (LV-AC-TEM) in combination with density functional theory (DFT) was performed to study open questions regarding the dynamics of extended defects in a two-dimensional (2D) transition metal dichalcogenide (TMDs) bringing together two groups of theoretical and experimental researchers from Germany and Finland. Based on atomic-resolution data measured with the Cc-Cs corrected SALVE microscope observed and modeled the in situ formation of atomic defects and their dynamics in 1H-MoTe₂ and also analyzed whether it is possible to induce these transformations in a controllable manner using electron irradiation in the TEM at a very low accelerating voltage of 40 kV.

“Understanding the transformations of 2D materials under an electron beam may potentially open new pathways for defect-based engineering of devices such as single-photon emitters, quantum dots, and metallic vacancy lines embedded into semiconducting 2D material,” said the authors. “We were able to follow the migration of atoms on the atomic scale and to understand the migration and agglomeration of single Te vacancies with the help of supporting DFT calculations.”

2D TMDs can exist in different phases, as trigonal prismatic (H), octahedral (T), or monoclinic (T′) phase structures. (1, 2) 1H-TMDs have a hexagonal lattice with alternating metal and chalcogen atom columns, wherein the two chalcogen atoms are on top of each other. In the 1T-TMD phase, the chalcogen atoms of the first chalcogenide layer are located in the center of the hexagonal rings of the second layer. However, in group-VI chalcogenides, this phase should transform to the lower-energy distorted 1T′-phase. (1) Transformations from 1H to the 1T′-phase can be induced using several approaches, for example, by electrostatic doping or atomic defect creation. (3)

Molybdenum ditelluride (MoTe₂) is one of the most interesting 2D TMDs as the energy difference between the semiconducting 1H and the metallic 1T′-phase is only ∼31 meV per unit cell; (4) therefore, a phase transformation can easily be induced by heating, (5) electrostatic gating, (6) doping, (7) or adsorption of atoms. (8) Using atomistic simulations, Duerloo et al. (4) predicted that mechanical deformations can cause a switch between the semiconducting and the metallic phase in single-layer TMDs such as MoTe₂. Uniaxial tensile strains along the b axis (armchair direction) ranging from 0.3 to 3% should transform MoTe₂ from the 1H to the 1T′-phase already at room temperature. (4)

Crystalline imperfections, such as vacancies, in 2D MoTe₂ can induce a phase transformation between the 1H and 1T′ phases. (6) A substantial amount of knowledge on the behavior of intrinsic and extrinsic defects, such as vacancies or impurities, has been obtained. (9, 10) Many insights came from the high-resolution transmission electron microscopy (HRTEM) experiments, which allow “seeing” every atom in the 2D system and following defect structure evolution in real time. Defects can deliberately be produced by the electron beam. In particular, the investigations for single-layer MoTe₂ showed that point defects induced in one chalcogenide layer agglomerate mainly into single vacancy lines, whereas defects in both chalcogen layers are predominantly forming extended defects. (10) Defect-mediated transformations from the 1H into the 1T′ phase, the formation of inversion domains with mirror twin boundaries, and complicated extended defects, which can be referred to as quantum dots, have been observed under electron irradiation. (10)

In their new study, which can be referred to as a follow-up work of a previous paper (10), the authors addressed the open issue: (i) how do extended defects migrate and what elementary migration events are responsible for sliding and rotating single vacancy lines, forming inversion domains, and local transformations to the 1T′-phase? (ii) How do external factors such as strain govern the evolution of complex defects? (iii) What are the energy barriers for these processes? (iv) Is it possible to induce these transformations in a controllable manner using electron irradiation in the TEM?

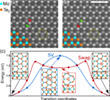
To establish a link to the previously published HRTEM data on the behavior of isolated point defects in MoTe₂ (10) and their study of multiple vacancy defects, the authors analyzed the defect diffusion by considering the migration of vacancies and their agglomeration into extended defects. Figures 1-5 show Cc/Cs-corrected 40 kV HRTEM images of freestanding 1H-MoTe₂. The honeycomb structure in Figure 1a,b is constructed by Mo atoms (indicated by turquoise dots in the bottom left) and brighter Te2 columns (indicated by orange dots). Red arrows mark a single vacancy (V1Te). Orange arrows describe the movement of an atom through the lattice and the shift of Te2 columns are indicated by the black arrows. The authors analyzed the migration of dislocations, starting from a single vacancy to the migration of longer vacancy lines through the lattice.

Migration of a single vacancy

In Figure 1a to 1b, a migration step of a V1Te within the same chalcogen layer is illustrated. A V1Te consists of a single missing tellurium (Te) atom in a Te2 column, which results in about half of the contrast compared to a Te2 column. A second V1Te, which was fixed in position during the recording time, is shown by a yellow dotted ring for better identification of the Te atom migration path. Due to the atomic lattice symmetry, the three surrounding nearest-neighbor Te atoms in the same chalcogen layer are equally likely to migrate and occupy the single vacancy.

In Figure 1c, the calculated minimum energy pathways of the in-plane single vacancy migration (blue curve) and the single vacancy swap from one chalcogen layer to the other, which can also be referred to as migration perpendicular to the sheet (red curve), are shown. The pathway for the diffusion of an atom in the same side of the layer proceeds over a hexagon center to a nearest-neighbor single vacancy site. Here, the maximum energy barrier is about 1.6 eV, which is lower than the energy (4.87 eV) needed to displace one Te atom. (10) Moreover, the migration energy barrier is too high for thermal migration at room temperature, which indicates that the electron beam induces atom migration. (11) In MoTe₂, the maximum kinetic energy transferred from 80 keV electrons to the nucleus is about 1.48 eV, which is in the energy range (cf. Figure 1c) needed to enable the V1Te migration, (11) especially when lattice vibrations are taken into account, resulting in an initial kinetic energy of the atoms within the MoTe₂. At electron-beam energies of 40 keV, the maximum energy of 0.72 eV can be transferred, which should not be enough to break the intralayer covalent bonding between the metal and chalcogenide atoms, even with lattice vibrations. However, it was shown that electronic excitations in general (12) and specifically a combination of inelastic scattering mechanisms could reduce the threshold energies so that atom removal and migration below the “ground state” energy barriers can be induced. (13) In addition, the occurrence of further defects in the nearby neighborhood of a vacancy can lower the energy barrier. (14)

The kinetic pathway barrier of atom swapping (cf. red curve in Figure 1c) is similar in height to the sliding of a single Te atom to occupy a single vacancy. The authors assumed that “swapping” of single atoms in single vacancy lines occurs less likely than migration of atoms on one side of the single-layer. This assumption can be attributed to the fact that vacancies in both chalcogenide sides of the single-layer agglomerate to extended defects composed of column Te vacancies, including rotational trefoil-like defects.(10)

2-Vacancy Line Sliding and Rotation

Figure 2 shows a 40 kV Cc/Cs-corrected HRTEM image of V1Te, which is rotating from (a) to (b) around another V1Te, which together form the shortest possible vacancy line. Red arrows mark the vacancy lines constructed of single Te vacancies in all the following HRTEM images. The vacancy line can be rotated by multiples of 60°, with the orientation along any of the zigzag directions of the hexagonal lattice structure in a 1H-MoTe₂ single-layer. However, the clockwise and anticlockwise rotations will traverse through different atomic environments (a Mo atom on one side of the vacancy line and a hexagon center on the other), which yield different migration barriers. The structure shown in Figure 2c illustrates the two main migration paths, and the diagram in Figure 2d presents the corresponding calculated energy pathways of the two possible atom migrations. In both paths, the Te atom migrates via the center of the hexagonal ring, where it is surrounded by zero Te atoms in path-1 and one Te atom in path-2, as was also discussed earlier for MoS2. (11) The path-1 transition state configuration appears locally similar to the 1T-phase, which in MoTe₂ is energetically very close to the 1H-phase, while the path-2 transition state configuration experiences “repulsion” from the neighboring Te atoms. Indeed, as evident from the calculated barriers presented in Figure 2d, path-1 should be more probable than path-2. Path-1 consists of three steps: first, the energy of ∼0.15 eV is required to break bonds and force the atom into the intermediate state, where the atom rests in the center of a hexagon. Second, a maximum energy barrier of ∼0.18 eV needs to be exceeded to rotate the local bonding motif, which experiences symmetry breaking due to Jahn–Teller distortion. In the last step, a ∼0.07 eV barrier follows for the Te atom to return from the center of the hexagon to the normal Te site. Since atomic reactions take place in the range of femtoseconds and exposure times in the range of seconds are necessary to reach an interpretable signal-to-noise ratio, the individual steps of the migration cannot be captured. As an example, we have shown in Figure 2a to 2b the time period of 3 s.

These two directions of motion (path-1 and path-2) are fundamental for explaining other movements of line defects. This is clearly shown by the second example in Figure 2e,f, in which the sliding of an equally long vacancy line (V2Te) to a neighboring lattice position is demonstrated. The calculated migration path (not shown) indicates that the sliding occurs via sequential path-1 and path-2 events (i.e., two sequential rotations) instead of a concerted movement. To mark the two-step process, arrows in the pathway colors (orange for path-1 and light blue for path-2) are inserted in (e). The direction of motion in this example suggests that to keep the two vacancies in the nearest-neighbor sites, a path-1 event must occur first, followed by a path-2 event.

4-Vacancy Line Sliding and Rotation

That same consideration can also be used to understand the migration of longer vacancy lines through the lattice, as illustrated in Figure 3. Structure models in Figure 3a show the individual steps during the sliding of a single vacancy line with four missing Te atoms (V4Te). Single vacancies are marked with red dotted rings. Colored arrows show the direction of movement of the involved atoms to fill the marked vacancies. Orange arrows describe the movement of an atom through the lattice with a path-1 event and light blue arrows a path-2 event. The position of the Te vacancy line during the movement is marked with red arrows in the starting and final structure models. To move the entire line through the lattice, four individual events must be carried out. Figure 3b,c shows the corresponding 40 kV Cc/Cs-corrected HRTEM images of vacancy lines with four missing Te atoms. With respect to the yellow marked point defect, the vacancy line slides diagonally through the lattice from (b) to (c). In the zigzag direction, the distance corresponds to 3.5 Å and along the projection in the armchair direction to 3 Å. Figure 3d shows the calculated energy pathway of the sliding vacancy line for the steps shown in Figure 3a. The three path-1 steps (I–III) have a small barrier as in the case of V2Te and thus expected to proceed fast, whereas the last path-2 step has a fairly high barrier. Even though four Te atoms are involved in the sliding process, the maximum energy barrier (∼1.5 eV) is even lower than for the V1Te migration (∼1.6 eV, see Figure 1c). Due to the hexagonal symmetry of the atomic lattice, the single vacancy line can also slide in the opposite direction. However, in this case, the order of migration steps is inverted: first, one path-2 step and then three path-1 steps.

Figure 3e–g shows an example for the rotation of a single vacancy line consisting of V4Te. In the new experiments, the authors observed that the rotation of single Te vacancy lines can be formed by up to five vacancies. Occasionally, the authors observed relatively stable 1T′-phase islands, as shown in Figure 4, where a single Te vacancy line transforms to a trapezoidal 1T′-phase region. To clarify the positions of the atoms, an overlay of the structures in (a) and (b) is inserted, as shown in the corresponding panels below. The structure of the 1T′-phase is similar to that shown in Figure 3g. Also, Figure 3g shows that transforming it back to the vacancy line requires overcoming relatively large barriers according to their observed stability.

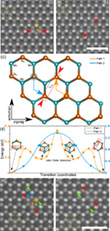
The DFT calculations that the authors performed sheded more light on the detailed paths of the transformations. For a rotation of a V4Te line, their DFT calculations resulted in two different possible migration processes. First, the rotation can be achieved by a step-by-step execution event. Or, second, all involved atoms move into a hexagonal center in the structure so that a triangular 1T-phase is formed (cf. inset in Figure 3g), from which the atoms can reorient themselves and rotate the vacancy line. The energy pathways for the two exemplified migration processes are shown in Figure 3g. While the triangular 1T-phase has low energy, the migration barriers to that configuration are much higher than for the path-1 events. The rotation occurs very fast, and no fully developed triangular intermediate state (as shown in Figure 3g, middle inset), where the tellurium atoms are located in the center of the hexagons, could be imaged experimentally. This supports the notion that the rotation process proceeds via sequential events. The results indicate that these events occur very fast, one after another, but after most of the attempts, the system returns to the original vacancy line configuration.

To understand the driving force for the observed transformations, the authors then investigated the development of strain around line defects and the effect of the transformations may strongly depend on the origin of the strin in the 2D materials and their heterostructures. (15) It was already known that there is a fundamental difference between the “standard” approach where strain is created externally, by using, for example, an atom force microscope (AFM) cantilever or deposition on elastomeric substrates (16) and the situation in an electron microscope, where strain naturally comes from the point and line defects created by the electron beam. To understand the transformations, the scientists analayzed strain of line defects and tensile strain. In total, the larger the occurring strain in the uniaxial-y direction, the more energetically favorable the rotation becomes.

Strain Analysis of Different Line Defects

We found that locally induced lattice distortions nearby a single Te vacancy line strongly depend on their length, as shown in Figure 5a. The distortion dependence due to strain perpendicular to the vacancy line results in a shift of the neighboring Te atoms to no longer be arranged in a column.

Lattice strain was measured in the line scan between the signal of the Te2 columns in the pristine lattice (red dashed lines) and the shift of the corresponding Te2 columns due to the vacancy lines indicated by the black arrows. The lattice strain was estimated to be 1.9% for a V2Te line and goes up to 7.2–7.4% for vacancy lines with four or six missing Te atoms. In the V2Te line example, a shift between the two nearest-neighbor Te2 atom rows is not visible in the HRTEM image but in the line scan where the third Te2 peak from the left is slightly shifted from the red dashed line (indicated by the black arrow). For the V4Te line, the intensity peaks between the Mo and Te2 column are not distinguishable anymore because the two Te atoms are strongly shifted apart from each other, resulting in a broadened peak in the intensity profiles for the second Te2 column from the left. The same effect can be seen for the V6Te line.

DFT-based optimized structures of an infinite single Te vacancy line in the top and side views are depicted in Figure 5b. To distinguish between long- and short-range strain fields at an infinite single Te vacancy line, we performed DFT strain simulations shown in (c). The calculated strain map indicates the induced lattice strain by colors, where the red area represents expansion and blue stands for compression. The maximum lattice expansion and compression within the structure are of the order of 3%. The overall strain caused by such an infinite single vacancy line induces a lattice distortion of 8%, which is very close to the experimentally obtained values for the listed V4Te and V6Te single vacancy lines in Figure 5a. The maximal lattice distortion of 8% can be appreciated in the side view of the infinite single vacancy line in Figure 5b.

Tensile strain and 4-Vacancy Line Strain-Dependent Rotation

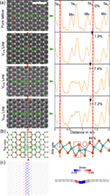
To understand the energetics of the phase transformation in more detail, the authors then analyzed between the formation energies on the example of the 1T′-phasevacancy line (cf. Figure 7a). The results in Figure 7b suggest that the formation energy per missing Te atom for single vacancy lines is lower than for the trapezoidal 1T′-phase although the difference in the formation energies per Te atom between the single vacancy line and the local 1T′-phase gets smaller with the increasing length of the vacancy line. As the transformation effect has been observed more often in longer line defects, these experimental results were confirmed by the DFT calculations of the scientists.

Although single Te vacancy lines are formed under the electron beam and should be energetically more stable than the trapezoidal 1T′-phase island, the transformation was often observed, and the structure was remarkably stable under irradiation with energetic electrons. The authors that some of the phases, such as the 1T′-phase, may be stabilized by strain. The calculated lattice constants are a = b = 3.54 Å for the 1H-phase and a = 3.48 Å and b = 7.23 Å for the 1T′-phase. Embedding a 1T′-phase region within an unstrained 1H-phase matrix thus means that the 1T′-phase region is tensile strained along a and compressively strained along b.

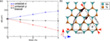
In the literature, some the scientists had previously chosen the hybrid Hartree–Fock/DFT method with the Heyd–Scuseria–Ernzerhof functional (4) as an exchange–correlation functional. This functional gave lower stress values than the PBE/DFT approach that the authors had used in their new study to interpret their atomically resolved AC-HRTEM data. Furthermore, impurities and entropic contributions to the free energy at finite temperatures can also play an important role, facilitating the transition to the T′-phase. (17) The previosu simulations (4) had indicated that other components of strain and finite temperatures substantially reduce the critical strain value. While we know that vacancies induce tensile strain, a precise value is difficult to estimate.

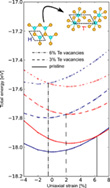
The new data the authors presented now, see Figure 8, clearly indicated that the introduction of Te vacancies lowers the required strain for a phase transformation in 1H-MoTe₂. Based on these results and assuming that the migration barriers shown in Figure 3g are not dramatically increased by the presence of small tensile strain, the most probable explanation is that the strain and the presence of Te vacancies result in a phase transformation that is further facilitated by electron beam-induced bond breaking at a very low acceleratiing voltage of only 40 keV.

In summary, the authors had addressed many open questions related to the transformation pathways to complex defect structures such as single Te vacancy lines and small islands of the 1T′-phase. Their experimental data combined with the results of DFT calculations revealed that (i) all migrations of vacancies and extended defect structures can be deconstructed to two paths of motion of single Te atoms through the hexagonal crystal lattice. This step-by-step process leads to an even lower energy barrier for the movement of single Te vacancy lines than for individual single Te vacancies. The observed elementary migration events of the defect structures are likely further accelerated by the energy transfer from the electron beam. (ii) The apparent changes in the preferred orientation of the line defects and stability of 1T′-phase regions are related to the development of strain in the sample, induced by the formation of vacancies that are the atoms sputtered by the electron beam.

From the new results it became evident how energetic electrons provide the possibility to create defects and modify their density and in general their arrangement in atomically thin MoTe₂. The new findings should enhance the control over defects. "Mechanical strain can come not only from the defects but also be created externally. A synergetic can be experimentally achieved by combining TEM with a scanning tunneling microscope (STM) or an atom force microscope (AFM) located inside the TEM chamber", Ute Kaiser who led the TEM studies at the University of Ulm said. On a large scale (but without in situ control of defects), defects can be produced by ion irradiation (18) and then strain can be applied by bending the substrate (16) or using AFM. (19) The understanding of defect dynamics in 2D transition metal dichalcogenides should facilitate tailoring their local optical and electronic properties.

Resource: Janis Köster, Mahdi Ghorbani-Asl, Hannu-Pekka Komsa, Tibor Lehnert, Silvan Kretschmer, Arkady V Krasheninnikov, Ute Kaiser. Defect Agglomeration and Electron-Beam-Induced Local-Phase Transformations in Single-Layer MoTe₂ (2021) The Journal of Physical Chemistry C 125, 13601-13609, doi: 10.1021/acs.jpcc.1c02202, [PDF].

References

Chhowalla, M.; Shin, H. S.; Eda, G.; Li, L. J.; Loh, K. P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263– 275.
Pizzochero, M.; Yazyev, O. V. Point defects in the 1T′ and 2H phases of single-layer MoS2: A comparative first-principles study. Phys. Rev. B 2017, 96, 245402.
Lehnert, T.; Lehtinen, O.; Algara-Siller, G.; Kaiser, U. Electron radiation damage mechanisms in 2D MoSe2. Appl. Phys. Lett. 2017, 110, 033106.
Duerloo, K.-A. N.; Li, Y.; Reed, E. J. Structural phase transitions in two-dimensional Mo- and W-dichalcogenide monolayers. Nat. Commun. 2014, 5, 4214.
Brown, B. E. The crystal structures of WTe2 and high-temperature MoTe₂. Acta Crystallogr. 1966, 20, 268– 274.
Cho, S.; Kim, S.; Kim, J. H.; Zhao, J.; Seok, J.; Keum, D. H.; Baik, J.; Choe, D.-H.; Chang, K. J.; Suenaga, K. Phase patterning for ohmic homojunction contact in MoTe₂. Science 2015, 349, 625– 628.
Wang, Y.; Xiao, J.; Zhu, H.; Li, Y.; Alsaid, Y.; Fong, K. Y.; Zhou, Y.; Wang, S.; Shi, W.; Wang, Y. Structural phase transition in monolayer MoTe₂ driven by electrostatic doping. Nature 2017, 550, 487– 491.
Zhou, Y.; Reed, E. J. Structural phase stability control of monolayer MoTe₂ with adsorbed atoms and molecules. J. Phys. Chem. C 2015, 119, 21674– 21680.
Komsa, H. P.; Kotakoski, J.; Kurasch, S.; Lehtinen, O.; Kaiser, U.; Krasheninnikov, A. V. Two-dimensional transition metal dichalcogenides under electron irradiation: Defect production and doping. Phys. Rev. Lett. 2012, 109, 035503.
Lehnert, T.; Ghorbani-Asl, M.; Köster, J.; Lee, Z.; Krasheninnikov, A. V.; Kaiser, U. Electron-beam-driven structure evolution of single-layer MoTe₂ for quantum devices. ACS Appl. Nano Mater. 2019, 2, 3262– 3270.
Komsa, H.-P.; Kurasch, S.; Lehtinen, O.; Kaiser, U.; Krasheninnikov, A. V. From point to extended defects in two-dimensional MoS2: Evolution of atomic structure under electron irradiation. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 035301.
Lee, C.-W.; Schleife, A. Hot-electron-mediated Ion diffusion in semiconductors for ion-beam nanostructuring. Nano Lett. 2019, 19, 3939– 3947.
Kretschmer, S.; Lehnert, T.; Kaiser, U.; Krasheninnikov, A. V. Formation of defects in two-dimensional MoS2 in the transmission electron microscope at electron energies below the knock-on threshold: the role of electronic excitations. Nano Lett. 2020, 20, 2865– 2870.
Sensoy, M. G.; Vinichenko, D.; Chen, W.; Friend, C. M.; Kaxiras, E. Strain effects on the behavior of isolated and paired sulfur vacancy defects in monolayer MoS2. Phys. Rev. B 2017, 95, 014106.
Novoselov, K. S.; Castro Neto, A. H. Two-dimensional crystals-based heterostructures: materials with tailored properties. Phys. Scr. 2012, 2012, 014006.
Castellanos-Gomez, A.; Roldán, R.; Cappelluti, E.; Buscema, M.; Guinea, F.; van der Zant, H. S. J.; Steele, G. A. Local strain engineering in atomically thin MoS2. Nano Lett. 2013, 13, 5361– 5366.
Kretschmer, S.; Komsa, H.-P.; Bøggild, P.; Krasheninnikov, A. V. Structural transformations in two-dimensional transition-metal dichalcogenide MoS2 under an electron beam: insights from first-principles calculations. J. Phys. Chem. Lett. 2017, 8, 3061– 3067.
Iberi, V.; Liang, L.; Ievlev, A. V.; Stanford, M. G.; Lin, M.-W.; Li, X.; Mahjouri-Samani, M.; Jesse, S.; Sumpter, B. G.; Kalinin, S. V. Nanoforging single layer MoSe2 through defect engineering with focused helium ion beams. Sci. Rep. 2016, 6, 30481.
Manzeli, S.; Allain, A.; Ghadimi, A.; Kis, A. Piezoresistivity and strain-induced band gap tuning in atomically thin MoS2. Nano Lett. 2015, 15, 5330– 5335.

Atom migration in MoTe2

Atom migration in MoTe₂