From Point Defects in Graphene to Two-Dimensional Amorphous Carbon.

Figure 1. Elementary defects.

March 09, 2011 – A team of scientists from Finland and Germany has studied the transformation of graphene into two-dimensional amorphous carbon. The observations, along with first-principles calculations, provide new insights to the bonding behavior of carbon and the dynamics of defects in graphene. The created domains possess a band gap, which may open new possibilities for engineering graphene-based electronic devices.

Figure 2. Multivacancy formation.

Aberration-corrected high-resolution transmission electron microscopy (AC-HRTEM) has recently allowed atomic-resolution imaging of regular carbon nanostructures and identification of defects in these materials [1,2]. Earlier experiments on curved carbon nanosystems [3,4] had shown that they avoid under-coordinated atoms under irradiation at high temperatures via vacancy migration and coalescence. The arrangement of other polygons can be geometrically deduced via the isolated pentagon rule (IPR) [5-7] and Euler’s theorem [8]. In fullerenes [5] and carbon nanohorns [6], nonhexagonal rings usually lead to the development of nonzero curvature. However, despite the recent advances, the precise microscopic picture of the response of graphene to electron irradiation remained incomplete.

Figure 3. DFT calculation.

Now the scientists made a new study with a spherical aberration-corrected FEI Titan 80–300 TEM, equipped with an objective-side image corrector. The microscope was operated at low voltage for HRTEM imaging, and at 300 kV for defect production, above the knock-on threshold of graphene [9,10]. The atomic scale study with underpinned with Density-functional theory (DFT) calculations.

Building a two-dimensional amorphous membrane

"This is the first time that anyone has systematically tried to transform and observe the transformation of a two-dimensional material from the crystalline to the amorphous state with that high precision.” says Jannik Meyer from the group of Electron Microscopy for Materials Science (EMMS) at Ulm University.

The scientists reported now the transformation of graphene into a two-dimensional random arrangement of polygons. Until now, experiments on graphene [2] reported only the development of holes. Only theoretical studies had also predicted the appearance of small holes or formation of haeckelitelike configurations [11] or dislocations [12].

Video 1: The transformation from a crystalline to an amorphous two-dimensional material created by a high-dose exposure of graphene to 100 kV electrons.

They show that the transformation are driven by two simple mechanisms: atom ejection and bond rotation. They also discovered unexpected configurations, such as stable carbon tetragons [13] which appear upon linear arrangement of divacancies. Contrary to the expectations, the material did not collapse but remained stable.

The challenge of studying undercoordinated systems

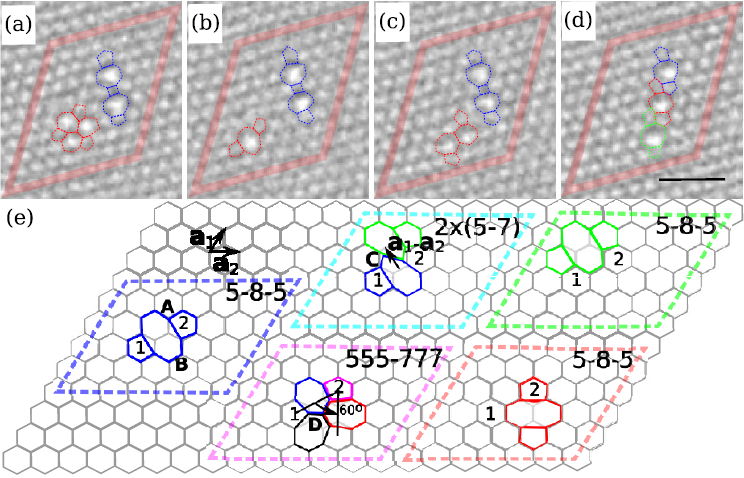
To understand the mechanisms of the transformation, the scientists separated them by varying the electron beam energy. They created initial damage in a graphene sheet by a brief 300 kV irradiation. Then they studied them at 80 kV, where pristine graphene remains stable, but under-coordinated atoms can be still be ejected (T_d for a sp²—bonded C is about 18–20 eV [9,10]). Also bond reorganization is still possible, as activation energies for bond rotations in sp²—bonded carbon structures are in the range of 4–10 eV [14-16] (Figs. 1(a) and 1(b)) resulting in the formation of the Stone-Wales defect [17], and lower votages are desired to observe defective graphene. Furthermore, defect structures, such as divacancies, can be produced (Figure 1).

A brief exposure to a 300 kV beam (dose ~10⁷ e^-/nm²) creates mainly mono-vacancies, which then convert to divacancies. Because atom ejection occurs at random positions, vacancies initially appear randomly in the area exposed to the electron beam. During the image sequence at 80 kV the vacancies start to migrate. Each migration step is initiated by a single electron impact from which the atom obtains energy slightly below T_d. In other words, electron irradiation provides the activation energy to drive the system from a local energy minimum into another one.

Figures 2 shows a collapse of linearly clustered defects into an apparently less defective structure with a dislocation dipole. This effect has earlier been predicted for graphene [12]. During continued irradiation, the scientists now observed the formation of a cluster of rotated hexagons surrounded by a chain of alternating pentagons and heptagons. Such configurations, rotated by 30° with respect to the original lattice and matched by pentagons and heptagons to the zigzag lattice direction, seem to be the preferred way to incorporate missing atoms in the graphene structure. Because of the matching numbers of pentagons and heptagons—and hence cancellation of negative and positive curvature—these structures remain flat.

To understand the transformations, the scientists calculated the formation energy of the experimentally observed structures using DFT. [18-23] The lowest-energy tetra-vacancy (four missing atoms) can be created by combining two V₂ (5555-6-7777) divacancies, whereas the hexavacancy (six missing atom) requires three of these defects (Figure 3). Remarkably, these configurations have the lowest formation of any reported vacancy structures with equal number of missing atoms in graphene. A hole with six missing atoms has formation energy of ~6 × 3.15 eV, while for a dislocation and haeckelitelike structure values of ~6 × 3.72 eV and ~6 × 2.64 eV have been reported earlier [12]. The rotated-hexagon defects spawn the family of lowest-energy multivacancies in graphene.

The richness of carbon continues to surprise

The new material can be termed amorphous graphene might be interesting for applications but again provides new insides in fundamental physics. The scientists showed that in contrast to the zigzag-oriented divacancy [24], the rotated-hexagon defects open a band gap in graphene, as can be seen from the density of states in Fig. 3. The calculated band gap is in the order of 200 meV. More advanced DFT methods shall be applied to further investigate the new material in the future [25].

“Due to increased reactivity amorphous two-dimensional carbon may also be exploited for functionalization of graphene.” Ute Kaiser, says. “Clearly, despite the large amount of research, the richness of carbon chemistry continues to provide surprises. The understanding of the driving force for the transformations is also an essential step to control radiation damage which is a central goal of every electron microscopist.”

Highlighted Topics

Electron divacancy migration

Individual transitions can lead to structures with higher energy. For example, the intermediate states for the divacancy migration (dislocation dipole (Fig. 4(c)) and V₂ (555-777) (Fig. 4(a))) have formation energies E_f, which differ from that of the V₂ (5-8-5) by~+ 3.72 eV and ~- 0.66 eV, respectively. Aligning divacancies along the zigzag direction of the lattice (Fig. 4(d)), ~1.32 eV of energy is gained per a divacancy pair, as compared to isolated divacancies. When the alignment appears along the armchair direction (Figs. 4(a)–4(c)), the energy gain is 2.01 eV. In this case, a tetragon is formed where the two pentagons of the adjacent divacancies would overlap. HRTEM simulation of the DFT-optimized structure of the defect is in agreement with the experimental image. Note that sp²—bonded carbon tetragons in molecules, as in cyclobutadiene, can be stabilized only at low temperatures and when the molecules are embedded into a matrix [13]. Here, they are stabilized by the surrounding graphene lattice, as theoretically predicted for nanotubes [26].

Fig. 4: (a)–(d) Electron beam driven divacancy migration observed at 80 kV. In (e), the changes in the bond configuration required for allowing the migration of a divacancy are shown. Transformation V₂ (5-8-5) → 2 × (5-7) is initiated by rotating bond A, and V₂ (5-8-5) → V₂ (555-777) by rotating bond B. Rotating bonds C and D will lead to the final V₂ (5-8-5) structures.

Resource: Kotakoski, J., Krasheninnikov, A. V., Kaiser, U. A. & Meyer, J. C. (2012). From Point Defects in Graphene to Two-Dimensional Amorphous Carbon. Phys. Rev. Lett., 106, 105505, doi: 10.1103/PhysRevLett.106.105505, [PDF], see also the [Supporting information].