Watching silica's dance: imaging the atomic arrangements in glass
November 25, 2013 - Developed in the 1930s, Zachariasen’s model is a description of the atom-arrangement in amorphous materials [1]. Recently, this old model was experimentally confirmed by Transmission Electron Microscopy and Scanning Tunnel Microscopy in two independent studies of silica glass at the atomic level [2, 3]. To observe the structural arrangement of a one-molecule-thick glass and to describe how it bends, deforms and melts, on the single-atom scale, the research teams led by Ute A. Kaiser, professor of experimental physics at University of Ulm, and David A. Muller, professor of applied and engineering physics and co-director of the Kavli Institute at Cornell for Nanoscale Science has now used the electron beam of a transmission electron microscope to image and excite atomic rearrangements and developed new atom tracking, respectively. For the first time, the researchers have directly imaged strain associated with individual rearrangements of atoms in silica glass and clarified the role of vacancies in shear deformations, as well as imaged and quantified the fluctuations at a glass/liquid interface [4].
Strain associated with individual rearrangements
As an example the scientists investigated the rearrangement of rings with 5-7-5-7 atoms into a 6-6-6-6 configuration that is shown in Figure 1B-E and the accompanying movie S1.
The trajectories shown in Fig 1F illustrate the movement of the individual atoms in Figures 1B-E. In order to determine the movement of atoms with high precision, the researchers eliminated the net movement from the images and fitted Gaussian functions at each atomic position and then determined the trajectories using particle-tracking programs from colloid research [5, 6]. Because 2D silica contains two superposed layers of SiO4 tetrahedra (see Fig. 1A) and since the contrast in the TEM image is mostly coming from the Si atoms, this method tracks the movement of Si-pairs in the 2D material. The two trajectories in the center of Figure 1F show the rearrangement of the central atoms of the 5-7-5-7 to 6-6-6-6 transformation, during which bonds break and new bonds are formed, i.e. plastic deformation occurs. In contrast, the surrounding atoms show smaller motion with respect to each other and keep their bonds with neighboring atoms, these are elastic deformations.
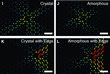
To understand the field of strain, in which the atoms are, molecular dynamics simulations of 5-7-5-7 to 6-6-6-6 ring transformations have been carried out using the large-scale atomic/molecular massively parallel simulator (LAMMPS) [5, 7].
Four simulations for (i) a crystal (ii) an amorphous material, (iii) a crystal at the solid-state edge, and (iv) an amorphous material at the solid state edge were performed (Fig. 2). The simulations showed good agreement with the measured displacements (Fig. 1H) for the case of ring transformations in an amorphous material at the solid state edge and furthermore, that elastic deformations are different at larger scales in crystalline and amorphous silica.
The role of vacancies in shear deformations
Plastic transformations play a key role in understanding of glasses. They are well know to occur in crystals leading to creation and migration of dislocations through the lattice. However for amorphous materials plastic deformations are not at all understood.
An example of a plastic deformation, a shear displacement is clearly visible in Fig. 3 when the trajectories of the atoms in region 1 (top left) and region 3 (bottom right) are compared (see Fig. 3A). The trajectories of the atoms in region 1 show hardly any change of position. An example is shown enlarged in Figure 3C. On the other hand, it is found in region 3 that the atoms have moved by 0.24 nm relative to the atoms in region 1. In the intermediate regions, there is a strong plastic ring rearrangement, see the regions 2 and 4, ((in region 2 alongside with vacancies, in region 4 alongside with the location at the edge of the solid see also the arrows in Fig. 3B)). In these regions, the shear displacement breaks, bindings between regions 1 and 3 occur, which allows their displacement against each other (see also movie S3). Our analysis suggests that shear transformations in other glass-like systems might also take place by rearrangement of covalent bonds at the shear interface.
The solid-liquid interface
In addition to the "solid-like" phase, another phase has been observed in which the atoms are much more mobile. As the atoms here are much more free to move so that no tension can arise, this phase is more like a liquid.
In Figure 4 it can be seen that most of atom movements in the solid phase occur at the boundary portions to the liquid phase (increased displacement in the solid phase is highlighted in red (see below the Fig. 4 B-D) [5]. Here, transitions between liquid and solid phases take place, wherein the atoms that are re-formed in the solid phase are unaffected from their previous solid state. During video recording, the length of the solid-liquid interface and the area of the solid fluctuate however without increasing or decreasing in total (Fig. S6, movie S4 and S5). This confirms that it is a stable state, and not the degradation of a solid state under electron beam radiation.
In brief
Using the electron beam in a low-voltage (80 kV) aberration-corrected high-resolution transmission electron microscope - to image and excite atomic rearrangements – in combination with profound image analysis and atom-tracking methods as well as atomistic modeling, a detailed picture of a two-dimensional glass was derived on the atom-by atom level. This opens a new way to study far-reaching and fundamental physics of glass materials. Furthermore, this two-dimensional glass offers in principle an opportunity to device fabrication when ultra-thin dielectrica are requested (note that reproducible silica films on metals can at present be fabricated at the Fritz-Haber Institute in Berlin, Germany).
Resource: Huang, P. Y., Kurasch, S., Alden, J. S., Shekhawat, A., Alemi, A. A., McEuen, P. L., Sethna, J. P., Kaiser, U., & Muller, D. A. (2013). Imaging Atomic Rearrangements in Two-Dimensional Silica Glass: Watching Silica’s Dance. Science, 342: 224-227, doi: 10.1126/science.1242248, [PDF], see also the Supplementary Information
-
Zachariasen, W. H. (1932). The atomic rearrangement in glass. J. Am. Chem. Soc., 54: 3841-3851.
-
Huang, P. Y., Kurasch, S., Srivastava, A., Skakalova, V., Kotakoski, J., Krasheninnikov, A. V., Hovden, R., Mao, Q., Meyer, J. C., Smet, J., Muller, D. A., & Kaiser, U. A. (2012). Direct imaging of a two-dimensional silica glass on graphene. Nano letters, 12: 1081-1086, doi: 10.1021/nl204423x
-
Lichtenstein, L., Büchner, C., Yang, B., Shaikhutdinov, S., Heyde, M., Sierka, M., Wlodarczyk, R., & Freund, H. J. (2012). The Atomic Structure of a Metal‐Supported Vitreous Thin Silica Film. Angewandte Chemie International Edition, 51: 404-407, doi: 10.1002/anie.201107097
-
Huang, P. Y., Kurasch, S., Alden, J. S., Shekhawat, A., Alemi, A. A., McEuen, P. L., Sethna, J. P., Kaiser, U., & Muller, D. A. (2013). Imaging Atomic Rearrangements in Two-Dimensional Silica Glass: Watching Silica’s Dance. Science, 342: 224-227, doi: 10.1126/science.1242248
-
Materials and methods are available as supplementary materials on Science Online.
-
Crocker, J. C., & Grier, D. G. (1996). Methods of digital video microscopy for colloidal studies. Journal of colloid and interface science, 179: 298-310, doi: 10.1006/jcis.1996.0217
-
Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. Journal of Computational Physics, 117: 1-19., doi: 10.1006/jcph.1995.1039